Nosé Dynamics
© Victor Anisimov, 2011
1. The notion of ensemble
Theoretical prediction of physical properties of materials from atomic structure is an important problem in material science. To constitute a material the system must consist of large enough number of particles so the forces responsible for macroscopic properties can be sufficiently present at atomic level to account for. Assuming that the selected size of atomic system is sufficient enough to be the source of macroscopic properties, the next thing to consider is the mathematical theory of atomic-level interactions. A system of N particles is fully defined by their 3N Cartesian coordinates by means of potential energy function representing energy of the systems as a function of particle coordinates. Despite the static picture is complete it provides no intuitive information about physical properties of the system, e.g. density, viscosity, etc. Although this information can be in principle obtained from the complete potential energy profile, it would require the evaluation of energy for each particle coordinate in the range from -∞ to +∞, which is entirely impractical.
Fortunately, there is another more convenient approach to determine physical properties of the system, which is called dynamics and which describes time evolution of the system. In it, instead of sampling the entire energy space of the system one may limit the consideration to the most relevant energy ranges. To define dynamic system one need to extend the 3N coordinate degrees of freedom of the system by 3N particle momenta. These combined degrees of freedom represent configurational space of the system. Among these degrees, particle coordinates determine potential energy of the system, whereas momenta determine kinetic energy of the system. Since kinetic and potential energy of the system are connected via Virial theorem (details of which should not concern us now), the knowledge of kinetic energy will be the factor limiting the potential energy sampling to those ranges which are relevant for the prediction of physical properties of the material. Through this we can avoid the need to find the entire potential energy profile as it is required in the static picture.
The sum of kinetic and potential energies gives the total energy of the system which must be conserved in a closed system having no energy exchange with the external environment. Dynamics which exactly preserves the total energy of the system, within accuracy of the numerical integration, generates configurations corresponding to microcanonical or NVE ensemble, which describes a system with constant number of particles (N), constant volume (V), and constant energy (E). Among these constants, the conservation of number of particles reflects the law of conservation of matter; the energy conservation represents the low of thermodynamics that energy cannot be created from nothing and cannot disappear to nowhere; lastly the particles are held together either by covalent bonds or due to periodic boundary condition, thus defining the constant volume of the system.
In NVE ensemble each microstate (particle configuration) completely describes a state of the system. It means that knowing a set of particle coordinates and momenta at any time moment is sufficient to fully describe time evolution of the system. The NVE ensemble consists of an infinite number of microstates each having the same total energy. Since the probability of finding a particular configuration is determined by its total energy, which is constant, it means that in NVE ensemble each microstate has the same probability of being encountered. As potential and kinetic energies evolve with time they simply flow one in another. Individually, potential energy and kinetic energy can assume whatever value as long as their sum is preserved. From this it follows an important conclusion that time average of potential or kinetic energy is not an observable property. As a consequence, microcanonical ensemble as whole cannot be characterized by temperature, since each individual microstate can have arbitrary instantaneous temperature with equal probability.
In classical mechanics the microstates cannot be strictly separated because all properties of classical system are continuous. The solution is provided by quantum mechanics, where system has discrete eigenstates. The ensemble approach combines all discrete microstates that lead to the same macroscopic property in a macrostate, thus connecting the atomic-level world with the macroscopic world through ensemble average. Although NVE ensemble does not correspond to experimentally observed conditions it provides an important theoretical tool upon which more elaborate ensembles are introduced.
The idea of ensemble average can be illustrated on the example of ideal-gas enclosed in a container. The pressure exhibited by particles of gas on the walls of the container continuously fluctuates over the time. On the other hand, the experiment measures average pressure over time. In the framework of ensemble, the time average of pressure can be replaced by average over the ensemble of microstates. Systems abiding to this rule are called ergodic. Thus ensemble provides a theoretical tool to connect thermodynamic (macroscopic) properties of the system with its microscopic structure.
Ensemble is defined in a phase space of all possible particle coordinates (q) and conjugate momenta (p). Phase space is a set of degrees of freedom in which all possible states of the system are represented. Each state of the system corresponds to a single point in the phase space. Probability distribution D(q,p) on the full phase space describes the probability of finding a particular microstate, which in case of microcanonical ensemble is
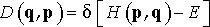 (1)
(1)
where δ is Dirac delta function, H is system Hamiltonian, and E is the total energy of the system. The delta function in Eq. 1 selects only those configurations which have total energy E. According to statistical mechanics, the probability of finding a state A among the possible states of the system is determined by its total energy. Since in microcanonical ensemble all microstates have the same energy, it explains why in NVE ensemble each microstate has equal probability.
A link between ensemble and thermodynamic properties of the system is provided by partition function, Z, which for a system of N identical particles gives the number of states the system can occupy at thermodynamic equilibrium
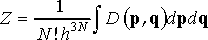 (2)
(2)
where h is Planck’s constant, and dp=dp1dp2…dpN and dq=dq1dq2…dqN. The expression in front of integral (Eq. 2) is a normalization factor. Since it is constant, we can skip it from the following analysis in order to keep the equations neat. In case of microcanonical ensemble, partition function is
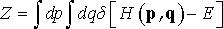 (3)
(3)
Despite of its theoretical significance, microcanonical ensemble has little utility for simulation of real systems since experimental measurements are typically performed under constant temperature and/or pressure conditions. Therefore particularly important is canonical ensemble, which describes the system at constant temperature, and which is a distribution over microcanonical ensembles.
It is insightful to compare microcanonical and canonical ensembles. If total energy in microcanonical ensemble is fixed, a system simulated under canonical ensemble is allowed to exchange energy with the external heat reservoir, called thermostat. Therefore in canonical ensemble only the average energy is fixed. The purpose of thermostat is to gently drive the course of dynamics into the particular area of condigurational space (q,p) where the system has the specific total energy range we are interested in. Canonical ensemble describes a system in which the total energy distribution is described by Maxwell-Boltzmann distribution and the probability density is
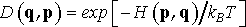 (4)
(4)
where kB is Boltzmann constant and T is equilibrium temperature. The partition function of canonical ensemble is
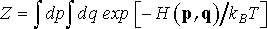 (5)
(5)
In this ensemble at thermodynamic equilibrium a physical property A of the system can be obtained as trajectory average denoted <A>
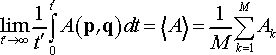 (6)
(6)
where M is number of trajectory snapshots, and Ak is instantaneous value of the physical property A computed for snapshot (microstate) k. The integral in L.H.S. of Eq. 6 typically cannot be solved analytically. Molecular dynamics provides the tool to solve it numerically via ensemble average.
2. Temperature in molecular simulation
Although temperature as physical property cannot be associated with microcanonical ensemble the simplicity of the latter provides a convenient condition to introduce the concept of temperature to dynamic system. In microcanonical ensemble the total energy of the system is the sum of kinetic and potential U(q) energies of the particles as described by the Hamiltonian
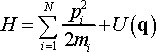 (7)
(7)
While the total energy is held constant, kinetic and potential energy terms can vary during the simulation. As particles collide and interact with each other during simulation a portion of their kinetic energy transforms to potential energy and vice versa. For the system of N particles, kinetic energy Ekin is determined by particle velocities, vi
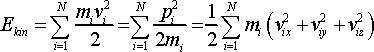 (8)
(8)
where mi is particle mass. In the R.H.S. in Eq. 8, particle velocities are represented in the form of their Cartesian components, vix, viy, and viz. At this point we break the connection with NVE ensemble, which we used above for the introduction of kinetic energy, and focus on the kinetic energy on its own, which is available in any dynamic system albeit through more complex mathematical expression.
Macroscopic equivalent of kinetic energy is the temperature of the system, T. To make a link between the kinetic energy of a system of particles and its temperature one needs an additional rule called equipartition theorem. This theorem says that each degree of freedom of the system contributes equally to kinetic energy in the amount of kBT/2 thus leading to the following relation between kinetic energy and temperature
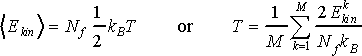 (9)
(9)
where kinetic energy is taken in brackets to represent ensemble average over M configurations; Nf is number of degrees of freedom, which is typically 3N, however, the exact number of degrees of freedom should be verified in each particular case. We will come back to this issue when discussing the number of degrees of freedom in particular cases.
Temperature is important physical parameter of the system. Relaxing the requirement of ensemble average for kinetic energy in Eq. 9 and dropping the sum one can introduce instantaneous temperature for each configuration, which can be defined for any dynamic system, including NVE one. Unlike the rigorous definition of temperature by Eq. 9, instantaneous temperature is an abstract value serving as a mathematical tool only. Since all states in microcanonical ensemble have equal probability and the value of kinetic energy is not limited to any specific range provided the total energy is maintained constant, NVE ensemble cannot be characterized by an average temperature during simulation. Henceforth the results of NVE simulation cannot be compared to the experimental measurement performed at the constant temperature. Considering this limitation of the NVE ensemble, it is very important to come up with a specific technique which would allow running dynamics at constant temperature.
There are different methods to control temperature in molecular dynamics. Particularly important is the extended system method in which additional degrees of freedom are added to the system Hamiltonian as reflected in the name of the method. Nosé extended the NVE Hamiltonian by adding kinetic and potential energy terms corresponding to the virtual degree of freedom of thermostat. According to Nosé the total energy of the extended system can be defined by the following Hamiltonian
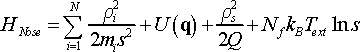 (10)
(10)
where qi and ρi are particle coordinates and momenta, respectively, mi is particle mass, s is virtual time scale variable, and ρs is its momentum; Q is a fictitious mass of the thermostat, Text is external constant temperature imposed by the thermostat, and Nf is number of degrees of freedom of this extended system. The reader might have noticed the use of peculiar notation for particle momentum, ρi, instead of familiar one, pi. The reason for that will be clarified in due course. For now we should keep in mind that these are different momenta.
For the first two terms in Eq. 10 an analogy can be drawn with the similar terms in the NVE Hamiltonian Eq. 7. Third and fourth terms in Eq. 10 describe the kinetic and potential energy of the virtual thermostat. The appearance of variable s in the expression of kinetic energy of the real particles in Eq. 10 is due to coupling of the particle velocities with thermostat.
Following is how thermalization is actually performed. Nosé Hamiltonian describes time evolution of the extended system in virtual time scale dτ. It can be mapped to real time scale dt through the relation
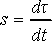 (11)
(11)
The ratio, s, between virtual and real time is treated as a dynamic variable, which means that time in Nosé dynamics is stretched. Real-time velocities vi of a particle are obtained by scaling of time derivative of coordinate qi as shown in dot notation
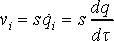 (12)
(12)
As we will see down further, via this scaling the kinetic energy of the real particles is driven toward temperature Text imposed by the thermostat.
Time evolution of the system is described by equations of motion defined for each degree of freedom of the system, which are the coordinates are momenta as functions of time. In Hamiltonian (NVE) dynamics these equations are obtained by differentiation of Hamiltonian (Eq. 7) in terms of conjugate coordinates and momenta
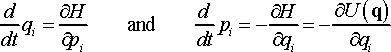 (13)
(13)
Such differentiation is possible because coordinates qi and conjugate momenta pi are treated as independent variables in time space. This formalism is most intuitive for a free particle moving in space under zero (or constant) potential, and for a static particle situated in the time-varying potential field. For the whole system encountering all particles and external fields the overall kinetic and potential energies are defined by the system Hamiltonian which couples kinetic and potential energies of individual particles. Thus, although particle coordinates and momenta are individually independent degrees of freedom, the system Hamiltonian and, through that, physical properties of the system depend on all of them together. It is like a geodesic map, although Cartesian coordinates x, y, and z defining the height of the land point are independent degrees of freedom the land surface of a particular area establishes a certain dependence between the coordinates.
The rules of Hamiltonian systems (Eq. 13) fully apply to Nosé Hamiltonian (Eq. 10) from which two extra equations of motion are produced for conjugate time scale variable s and its momentum ρs
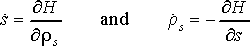 (14)
(14)
The complete set of equations of motion is derived as follows.
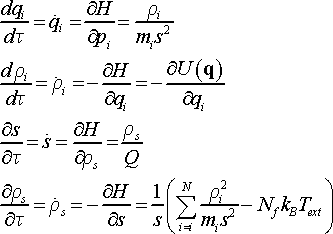 (15)
(15)
Since Nosé Hamiltonian is defined for virtual time τ, it is necessary to distinguish momenta in virtual and real time. The letter ρ denotes momenta in virtual time, whereas the letter p defines momenta in real time t.
In Hamiltonian dynamics the system Hamiltonian corresponds to total energy of the system, which is constant of time. Now we can show than Nosé dynamics in virtual time τ conserves system Hamiltonian. For that purpose we need to take time derivative of the Hamiltonian using the chain rule
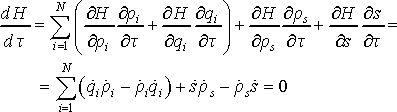 (16)
(16)
Since the derivative is zero the value of H does not change over time, and the total energy is conserved. This important result means that Nosé dynamics generates microcanonical ensemble in virtual time.
Having obtained equations of motion (Eq. 15) we can show now that temperature of the system in Nosé dynamics in real time corresponds to that of thermostat, Text. Translation of particle momenta in virtual time ρi to momenta in real time pi is defined by relation pi = ρi/s. Time derivative of momentum gives force (recall Newton equation dp/dt ≡ F) acting on the conjugate variable. The equation of motion for thermostat force
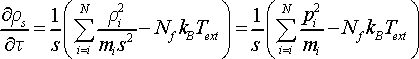 (17)
(17)
describes the rate of heat exchange between the real particles and thermostat. In R.H.S. of Eq. 17 the first term is the kinetic energy of real particles, and the second term is thermostat potential energy. If the sign of thermostat force (Eq. 17) is negative the energy will flow from the thermostat to the real particles. If the sign of thermostat force is positive the energy will flow in backward direction from the real particles to the thermostat. At the moment of thermodynamic equilibrium the thermostat force will be equal to zero
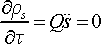 (18)
(18)
Combining Eq. 17 and Eq. 18 and using ensemble average one obtains
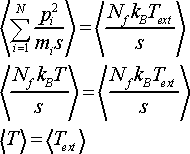 (19)
(19)
This shows that real particles in the system have kinetic energy which corresponds to the target temperature Text set by the thermostat. Thus in real time Nosé dynamics represents a simulation at constant temperature.
Ensemble having constant number of particles (N), constant volume (V) and constant temperature (T) is called NVT or canonical ensemble. Shown above is a simple proof that Nosé dynamics provides temperature stabilization. Although constant temperature is a necessary requirement for canonical ensemble, it is certainly insufficient for the dynamics to guarantee the generation of canonical distribution. In canonical ensemble energy distribution must correspond to Maxwell-Boltzmann distribution except for constant factor. For comparison, if total energy in microcanonical ensemble is fixed, a system simulated under canonical ensemble is allowed to exchange energy with the external heat reservoir. Therefore in canonical ensemble only the average energy is fixed. In order to prove that Nosé dynamics generates canonical ensemble we need to show that its probability distribution is defined by Eq. 4.
Recall that Nosé dynamics generates microcanonical ensemble when particle momenta ρi are defined in virtual time τ. This corresponds to the following partition function
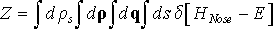 (20)
(20)
where dρ = dρ1dρ2…dρ3N and dq = dq1dq2…dq3N. Next we will show that Nosé dynamics generates canonical ensemble when particle momenta pi are defined in real time t. Since pi = ρi/s and ρi = spi, we have dρ = s3Ndp for 3N momenta.
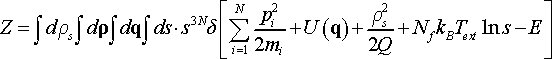 (21)
(21)
Because the expression in square brackets has only one zero as a function of variable s, which follows from the definition of phase space, we can utilize the following property of delta function
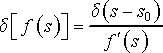 (22)
(22)
where f´(s) is derivative of function f(s), and where f(s0) = 0. The value of s0 can be found from the condition
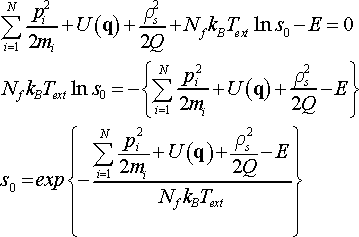 (23)
(23)
The derivative f´(s) is as follows
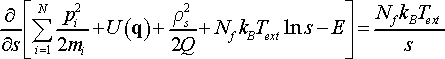 (24)
(24)
Note, pi is independent of s since s-dependence on particle momenta was eliminated during substitution ρi = spi. After application of the changes, the expression for partition function takes the form
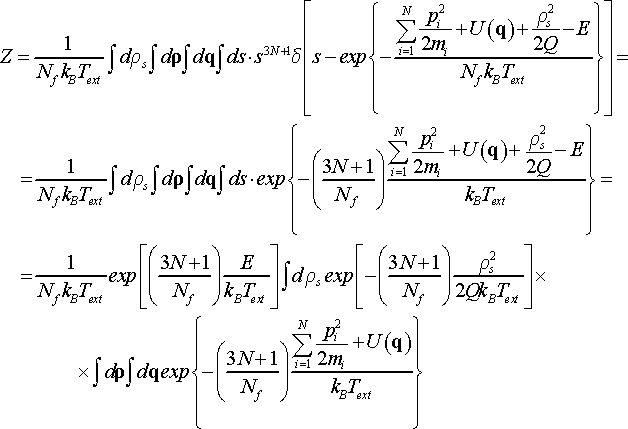 (25)
(25)
By choosing Nf = 3N + 1 and solving the integral for thermostat momentum, which is included in constant C, we obtain the partition function Z of the extended system corresponding to canonical ensemble
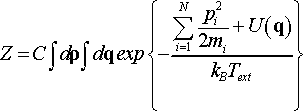 (26)
(26)
This proves that in terms of scaled momenta pi = ρi/s the Nosé dynamics generates canonical ensemble and has probability distribution function of the form
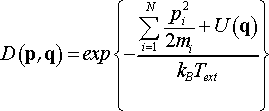 (27)
(27)
Eq. 25 also shows that in order to generate canonical distribution one has to use Nf = 3N + 1, where the extra degree of freedom corresponds to time scale variable s.
This completes a brief analysis of Nosé dynamics. Please use the link at the bottom of the page to leave your comments and suggestions.
